Introduce the lesson by having students think about functions in terms of inputs (x-values) and outputs (f(x)-values). Pose the following question:
Is it possible for a function to have an input (x-value) that has no corresponding output (f(x) value)?
[Yes, to be a function, each input must have a unique output.
However, there are many functions that have a limited set of inputs;
for example, f(x) = x½ is only defined for x ≥ 0, but each input has a unique output.]
Have students consider the question individually, then with a
partner. Instruct students to justify their answer with a graph or an
algebraic representation, along with a verbal description. Then, have
all students share their answers with a group. (This classroom strategy
is known as Think-Pair-Share, and it can be effective in getting
students to share their ideas with the entire class. By first testing
their ideas with a partner, students are more likely to then share with
the entire class.)
After students have considered the possibility that for many functions there exist x-values with no corresponding f(x)-values, distribute the Domain Representations Activity Sheet. Have students read the introduction at the beginning of the sheet.
 Domain Representations Activity Sheet
Domain Representations Activity Sheet
The first representation that students will use is a graph.
Students should use a graphing calculator to sketch the graph of each
of the eight functions. Have students include all necessary details of
each graph, including endpoints, asymptotes, and arrows.
Some students may have difficulty providing appropriate graphs
for functions which contain asymptotes. Explain to students that it is
inappropriate to use a vertical line as part of the function, because
it would no longer be a function. Ask students to investigate the
points at which they think a vertical line occurs; that is, have them
consider the x-values and corresponding f(x)-values at those points
The second representation students will use is a table. Students
can use the table function on a graphing calculator to complete the
table for each of the eight functions, or they can compute the values
by hand using any calculator.
Students may question why an ERROR message appears for some x-values
in some of the functions. Students should consider the algebraic
representation for the function. Students should notice that
substitution may result in taking the square root of a negative number
or dividing by zero. When students see an ERROR on the calculator, they
should record the error on their activity sheet as an E.
Once students complete all of the tables, have them answer the following questions:
- Examine the algebraic representations for the functions. Which
functions produce errors in the table? What types of functions have
errors?
[The square root and rational functions produce errors in the tables.]
- Why do square root and rational functions produce errors in the table?
[Taking the square root of a negative number and dividing
by zero are both undefined operations, and these operations occur for
some x-values.]
The third representation is a number line. Students will plot the x-values with corresponding f(x)-values on a number line.
Explain to students that whenever an x-value has a corresponding f(x)-value on the table, that x-value is said to be in the domain of the function. The set of all x-values with corresponding f(x)-values is called the domain of the function. Whenever an x-value produces an error for an f(x)-value on the table, that x-value is not in the domain of the function.
After students have completed the number line representations,
move students into groups of 2‑4. Have students compare their number
lines with those of their group members. Instruct each group to come to
a consensus with each number line. Assign each group to display a
number line on the board. Review the number lines by asking each group
to justify why they included particular x-values.
The fourth and fifth representations—verbal and symbolic.
Explain to students that the verbal description can be used to explain
the meaning of the symbolic, which is why these representations are
presented together.
After students have developed verbal and symbolic
representations, arrange students into new groups of 2‑4. Have students
compare their verbal and symbolic representations with those of their
group members. Instruct each group to come to a consensus with each
representation. Assign each group to put the verbal and symbolic
representations onto the board. Review the verbal and symbolic
representations by asking each group to justify why they included
particular x-values.
After reviewing verbal and symbolic representations, students
should examine the interconnections between all five representations.
They should compare the different representations side-by-side, to see
how they are related to one another. For instance, allow students to
compare the grapical and number line representations of the following
function:
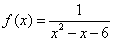
From these two representations, students should recognize that the asymptotes are x = ‑2 and at x = 3, and holes occur on the number line at ‑2 and 3. Further, errors occur in the table at these same x-values:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0.17 | E | -0.25 | -0.17 | -0.17 | -0.25 | E | 0.17 |
Finally, the domain of this function could be described verbally as "containing all x-values except ‑2 and 3," which symbolically can be represented as either x ≠ ‑2, 3, or as (‑∞, ‑2) ∪ (‑2, 3) ∪ (3, ∞).
Use the key questions below and others like them to help
students make connections between the five representations for each
function.
Questions for Students
1. Identify the functions with domain (-∞, ∞). Examine the graphical,
tabular, number line, verbal, and symbolic representations for each of
those functions. When a function has domain (-∞, ∞),
- Will the graph of the function contain an asymptote?
- Will the table of values contain an error?
- What can be determined about the number line?
- How is the function’s domain described verbally?
[The domain is uninterrupted, so there are no asymptotes,
no errors in the table of values, and no holes on the number line. The
verbal description should mention that the domain contains every
possible x-value.]
2. Identify the functions whose graphs contain asymptotes. Examine the
graphical, tabular, number line, verbal, and symbolic representations
for each of those functions. When a function’s graph contains an
asymptote,
- Will there be an error in the table of values? Explain why.
- What can be determined about the number line? Explain.
- How is the function’s domain described verbally?
- How is the function’s domain described symbolically?
[The asymptotes of the graph occur at the same x-values
for which an error occurs in the table, for which holes appear on the
number line, and for which the verbal description omits values.
Further, the symbolic representation will be divided into two or more
pieces, to indicate that some x-values are not in the domain.]
Teacher Reflection
- How did the different representations enhance students’ understandings of domain?
- When students worked in groups, were they involved in productive discussion/activity related to the representations?
- What role did the key questions play in students’ development of the connections between different representations?
- To what extent did students verbalize connections between the different representations?