To prepare for this lesson, draw a line on a sturdy plank of wood that
is 6 inches from one end. Then, draw additional lines at
12‑inch intervals. During the activity, students will stand with their
feet straddling these lines.
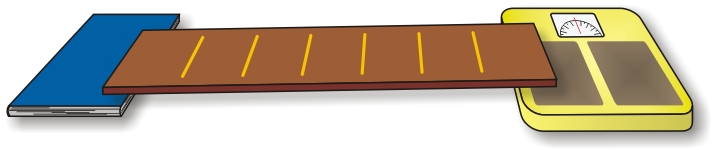
Place a bathroom scale and a textbook on the floor, about six feet
apart. Place the plank of wood so that one end rests firmly on the
scale and the other end rests on the book. The line drawn 6 inches from
one end of the plank should lie along the center of the scale. (Be sure
to test the arrangement prior to class to ensure that it is safe for
students.)
Provide the following explanation to students about the forthcoming
math investigation. (Since the lesson is called "Walk the Plank," it
may be fun to invoke a pirate accent while reading.)
Belay your talk, lads and lasses! Yo ho ho… ye all
have performed handsomely as math students, but I’m afraid there are
just too many of you in this here classroom. So today, some of ye are
going to walk the plank! (Point to the plank.) Aye, mateys! This here plank stretches between a scale and a textbook. Don’t ye be scared — it’s plenty sturdy. See? (Demonstrate its strength by walking across the plank.) As ye walk across it, we’ll record the weight shown on the scale. To show ye scallywags how to do it properly, I’ll go first.
Distribute the Walk the Plank Activity Sheet to students, and explain how the chart is to be filled in.
 Walk the Plank Activity Sheet
Walk the Plank Activity Sheet
Step on the plank so that your feet straddle the line down the
center of the scale. Read aloud the weight shown on the scale. (The
weight shown will be significantly more than your actual weight,
because it includes the weight of the plank.) On the chalkboard or
overhead projector, make a note of the weight.
Ask the class, "Do you think this is my actual weight?"
Students should realize that the weight shown on the scale includes the
weight of the plank. (Although it may seem trivial, this is an
important question to ask. When students realize that their actual
weight will not be displayed, they will be more likely to participate.
Still, when students walk the plank, use care with those who are
particularly self conscious.) Step off the plank.
Start at the line nearest the scale. Use the chart on the
activity sheet to record the weight. Step left, and move to the next
line on the plank. Again, read and record the weight. Continue moving
to the left and recording the weight at each line. If it becomes
difficult to read the weight, invite a student to read the weight as
you move across the plank. As you move and say the weight aloud, remind
students to fill in their charts.
After you have moved the entire way along the plank, ask the following questions:
- Plot the points on a graph. What do you notice? [The points occur
in a straight line; that is, the relationship between weight and
distance is linear.]
- Where is the y intercept? [The y‑intercept is approximately equal to the weight of the teacher plus the weight of the plank.]
- Where is the x intercept? [The x‑intercept is approximately equal to the length of the plank.]
- Approximately, what is the slope? Is it positive or negative?
[The slope is negative, and its absolute value is equal to the combined
weight of the teacher and the plank divided by the length of the
plank.]
Then, allow student(s) to walk the plank. If possible, select a
student whose weight is approximately half of your own weight. When the
line for this student is graphed, the slope of the line will be half of
the slope for your line. Then, select several other students at random.
(Because weight is a sensitive subject, choose students carefully, and
do not force any student to participate. To avoid an awkward situation,
you may want to ask for volunteers rather than select students.)
Allow students to discuss the questions on the activity sheet.
To fill the time and extend the thinking of those groups who finish the
worksheet and are waiting for others to finish, use the extension
activities below.
The activity sheet can be reviewed after all groups have
discussed the question, or you may have students complete it for
homework.
If necessary, you can refer to the Walk the Plank Answer Key.
 Walk the Plank Answer Key
Walk the Plank Answer Key
Questions for Students
1. Why is the slope of the graph negative?
[As the person moved away from the scale, the weight displayed on the scale decreased.]
2. Why does the weight shown on the scale not accurately reflect your weight?
[The weight shown will be significantly more than your actual weight, because it includes the weight of the plank.]
3. When a student whose weight was about half of the teacher's walked across the plank, what did you notice about the slope of that student's line on the graph?
[The slope of the line was about half of the teacher's line.]
Teacher Reflection
- Was students’ level of enthusiasm/involvement high or low? Explain why.
- What student actions allowed you to determine that students
did or did not have an adequate understanding of the material? How did
you use that information to adjust the lesson?
- Were you able to challenge the high achievers in your class?
If so, how? If not, what could have been done to provide more
challenge?
- Was this lesson appropriate for your students? If not, what could you do to make it more appropriate?