Pi Filling, Archimedes Style!

By calculating the areas of regular polygons inscribed and circumscribed about a unit circle, students create an algorithm that generates the never-ending digits of π, a common curiosity among high school students.

The purpose of this lesson is to use the geometry of regular polygons inscribed in and circumscribed about the unit circle to create an algorithm for generating the digits of π, known to be the area of the unit circle. The mathematical results are motivated by numeric examples, enabling students to investigate patterns in these numeric examples and to extend the results to the general case. Ultimately, students will investigate the inscribed and circumscribed methods simultaneously with a partner, and will determine which method provides a better approximation for the numerical value of π.

Students should consult with a designated partner when they have questions, get stuck, or need to check their results, but each student should do the mathematics and complete the Activity Sheet individually, unless otherwise noted. Each student will need a scientific or graphing calculator, an Activity Sheet, and scrap paper.

Students should already be familiar with the formula for finding the area of a regular polygon, A = ½(ap), where a is the apothem and p is the perimeter, and with the sine, cosine, and tangent functions before starting this lesson.

To begin the lesson, distribute the Inscribed and Circumscribed activity sheet and direct students to the four diagrams of a regular triangle, square, pentagon, and hexagon inscribed in unit circles. Briefly explain to students that Archimedes analyzed the geometry of regular polygons inscribed in unit circles, then note that the numbers of sides of the regular polygons starts with 3 (triangle) and increases by 1 side in each diagram. Ask students to predict what would happen when the number of sides of the regular polygons approaches infinity, and then have a few students share their predictions, as well as any other thoughts or questions that come to mind, with the class.

Inscribed and Circumscribed Activity Sheet

Though students will most likely have difficulty understanding the concept of a polygon with an infinite number of sides, asking them to think about this phenomenon will guide their thinking for the remainder of the lesson. Instruct students to keep these diagrams in mind throughout the lesson, because they will be asked to describe mathematically what happens as the number of sides in the regular polygons increases to infinity.

Actively guide students through the process of finding the area of the regular triangle first, following the steps below, as these steps will be replicated by students for other polygons. Ask leading questions that clearly communicate the connections between the prior step and the goal of the next step. A sample question of this form is: "We now know the base angles measure 30°. How does knowing this angle measure help us find the length of the apothem?"

Explain that the goal is to find the area of a regular triangle inscribed in a unit circle.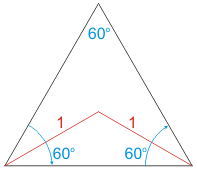

1. Consider the inner isosceles triangle below, formed by drawing two radii. Note that each base angle was 60°, from (n – 2) × 180/n, and the radii divide the base angles in half to form 30° angles.

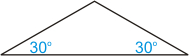
2. Next, form a right triangle by drawing the apothem (an altitude) from the center of the circle perpendicular to the base. Using the sine and cosine functions, the lengths of the apothem, y, and the base, 2x, can be found. Be sure to use the "degrees" setting on your calculator.

        

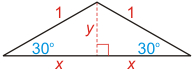
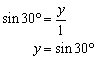
Consequently, the length of the base is 2x = 2 cos 30°, and the apothem is y = sin 30°.

We now have enough information to calculate the area of the inscribed regular triangle:

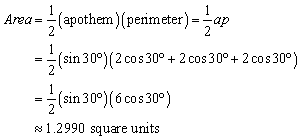
It is these last two lines, an exact expression for the area and its decimal approximation rounded to the ten-thousandths place value, that should be transferred to the table on the activity sheet. Throughout, it is very helpful to organize the calculations as written above, so students can see how the angle measure, perimeter, and apothem were calculated.

Working with their partners, instruct students to draw a picture of the regular triangle circumscribed about the unit circle, and then to work together with their partners in finding its area, following the same format as the inscribed triangle’s calculations. Circulate to each group, ensuring that they are on the right track. If students struggle to understand particular steps in finding the area, or are getting lost in all of the calculations, refer students to the picture of the circumscribed triangle. Reminding students of the geometric representation for their symbolic calculations can be an effective way to prevent confusion. The area of the circumscribed triangle is 3 ÷ tan 30° ≈ 5.1962, and should be transferred into the table on students’ activity sheets.

With students working together, direct the students to find the inscribed and circumscribed areas of the square. Check each group’s work to make sure they get an inscribed area of 2.0000 and 4.0000, respectively. Once each group has obtained the correct areas for the squares, have one student in each group find the area of the inscribed pentagon and circumscribed hexagon, with the other student finding the area of the circumscribed pentagon and inscribed hexagon. When each student has completed these two calculations, have each student analyze their partner’s calculations for correctness, discussing and debating each others’ work until both students agree that all four areas are correct.

Once students have completed the inscribed and circumscribed areas through the hexagon, ask students to look for patterns in their work, with the goal of generalizing an area function for the inscribed areas in terms of n. Watch for students who use an incorrect expression for the angle measures, as this is a common error. If students do not yet see the pattern, instruct them to calculate the area of the inscribed 7‑gon, and beyond if necessary, until this pattern becomes clear:

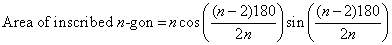
Watch for students who are unable to generalize to this function. Point out the similarities in their work, emphasizing the calculation of the perimeter and the apothem. Once the students obtain this function, they should use it to complete the rest of the table, including n = 50 and n = 200, and then should discuss Question 2 with their partner.

Teaching Tip: Watch for students who wonder what happens when this area function takes the value n = ∞. They may reason that when n = ∞, this area function reduces to n · cos 90° · sin 90° = n · 0 · 1, which has a value of 0. Students may wonder how the areas of the n‑gons increase, but when they reach infinity, the areas jump back to zero? The best answer is that ∞ is a strange concept, especially before students have taken calculus. Technically, the area function would reduce to ∞ · 0 · 1, which is indeterminate. Other indeterminate forms include 0/0, ∞/∞, ∞ · 0, 0⁰, ∞⁰, and 1^∞. One last curious result involving infinity would be to ask students to evaluate the fraction sin θ/θ as θ approaches 0. Revealing that the limit equals 1 is usually enough for students to accept that infinity doesn’t work like an ordinary "number."

Likewise, ask students to analyze the patterns in the circumscribed polygons’ areas, in order to define a general area function in terms of n. Students should discover this area function:

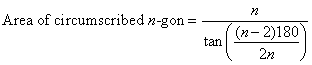
Students will complete this part of the lesson at different times, but all should be far enough along such that holding a class discussion will make sense to everyone. As students finish, point out that the circumscribed areas approach π just like the inscribed areas did, except they are always greater than π. Refer to the diagrams at the top the Activity Sheet to justify why the inscribed areas will always be less than the full area of the unit circle, and why the circumscribed areas will always be greater than the area of the unit circle. Emphasize that increasing n causes the regular polygons to become more "circle-like," which is why their areas approach the area of the unit circle, known to be π. An important question to ask students in this discussion is whether the areas will ever reach π. Drawing the distinction between the area being exactly equal to π, and the area matching the digits of π to a certain place value, is a common misunderstanding from students. Mention to students that this notion of a limit is the fundamental idea for studying calculus.

Teaching Tip: As an alternative method for generating results, you can have students use the table features on their graphing calculators. Students can generate the area of inscribed polygons in the first list and the area of the circumscribed polygons in the second list, and they can generate the perimeter of inscribed and circumscribed polygons in the third and fourth lists. Students should notice that the first and third lists approach π from below and the second and fourth lists approach π from above.

The final component of this lesson is to ask students which method they prefer for generating the digits of π. Emphasize that both methods, if continued for large enough values of n, will get arbitrarily close to the true value of π, but ask whether one of the methods is preferable. Valid responses include, but are not limited to:

• For each particular n (except n = 3), the circumscribed area is always closer to π than the corresponding inscribed area.
• Visually, the circumscribed polygons conform more closely to the circle. Another way to think about this concept is to look at the leftover areas compared to the unit circle. There is less area outside the circle and inside the circumscribed polygon; likewise, there is more area inside the circle and outside the inscribed polygon.

Students should be able to explain that the method of approximating π from circumscribed regular polygons is more efficient than from inscribed regular polygons.

For closure, select three students, one each to explain the following in their own words. (You can pretend that each student is explaining to a hypothetical student who was absent for this lesson.)

1. The work performed and discoveries from the inscribed areas approach.
2. The work performed and discoveries from the circumscribed areas approach.
3. How the inscribed and circumscribed areas are similar and different, and how both methods relate to approximating π.

Remaining class time can be spent with some of the assessment questions if only a few minutes remain, or pursuing one of the extensions if a significant amount of time remains.

 

Selected Solutions to the Activity Sheet

Question 1. The area formula for the inscribed regular n-gon is:

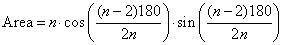
Question 2. For n = 3, the area is 1.2990. For n = 200, the area is 3.1411. As the value of n continues to increase, the area of the inscribed polygon will approach the area of the unit circle, which is π.

Question 4. Circumscribing regular polygons around the unit circle will overestimate the value of π, and therefore using these methods with circumscribed polygons will generate areas that approach π from above. The area formula is:

This lesson prepared by Jason Slowbe.