Sliding Triangle
The triangle at left lies on a flat surface and is pushed at the top vertex. The
length of the congruent sides does not change, but the angle between the two
congruent sides will increase, and the base will stretch. Initially, the area
of the triangle will increase, but eventually the area will decrease,
continuing until the triangle collapses.
What
is the maximum area achieved during this process? And, what is the length of
the base when this process is used to create a different triangle whose area is
the same as the triangle above?
This brainteaser was
written by Derrick Niederman.
Solution:
200 square units; 32 units.
For the first part of the question, the maximum area occurs
when the angle between the sides is a right angle. (This is often true for
geometry questions involving maximum area:
of all quadrilaterals with a given perimeter, the one with maximum area
is a square.) When the angle is a right angle, both the base and height of the
triangle are 20 units, so the area is 200 square units, which is
slightly more than the 192 square units of the original triangle.
For a more advanced trigonometry solution, remember that the
area of a triangle can be calculated by taking half the product of two sides
and the sine of the angle between those sides. Consequently, the area of any
triangle will be greatest when the sine of the included angle is greatest. The
sine function reaches its maximum, 1, when the angle is 90°, so a
right triangle will produce the greatest area.
For the second part of the question, note that if you bisect
the original triangle, divide it into two right triangles, and rearrange the
pieces, you can form a new triangle with exactly the same area. The original
triangle had a height of 16 (found through the Pythagorean theorem) and a
base of 24, so its area is ½(16)(24) = 192 square units. Likewise, the new
triangle has a height of 12 and a base of 32, so its area is also ½(12)(32) =
192 square units.

Again using a trig solution, A=(1/2)absinθ, where a and b are the side lengths. For the triangle
in this problem, a = b = 20. Consequently, the area of this
triangle is A=(1/2)absinθ=200sinθ, which has the graph shown below.
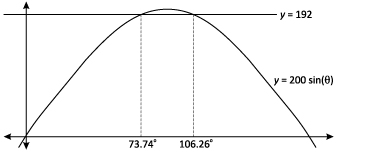
The original triangle has an area of 192 units, and the
line y = 192 crosses the graph of y = 200sin(θ) at two places — when
the included angle is 73.74° or 106.26°. The original triangle has an included
angle of 73.74°, and the other triangle with an area of 192 square units
has an included angle of 106.26°.