Solution: 3:36 and 11:20.  

The angle between the hour and minute hands equals the product of the hours and minutes at 3:36 and 11.20. In the latter case, the product equals 220, which is the number of degrees between the hands—if you go the long way around!

Let h = hours and m = minutes. The hour hand covers 30° every hour, so at the top of any hour it has traveled 30h degrees, and with every passing minute it travels another m/2 degrees. Given that the minute hand moves 6° every minute, the number of degrees between the hands is given by either 6m – (30h + m/2) or (30h + m/2) – 6m. Consequently, the relevant equations are:

 
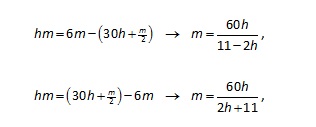
Because m is a positive integer, the first equation implies that 11 – 2h must divide evenly into 60h, and that happens only when h = 3. Plugging in h = 3 yields m = 36, so (3, 36), or 3:36, must have the desired property. Sure enough, there are precisely 3 × 36 = 108° between the hour and minute hands at 3:36.

For the second equation, the right-hand side must be a positive integer, and that happens only when h = 11. In that instance m = 20, producing (11, 20), or 11:20, as our second time. The fact that you go the “long way around” in this instance arises because the second equation essentially reverses the order of the hour and minute hands.